BILANGAN BERPANGKAT DAN BENTUK AKAR
BILANGAN BERPANGKAT DAN BENTUK AKAR
A. Bilangan Berpangkat
Bilangan berpangkat dibedakan menjadi dua macam, sebagai berikut.
1. Bilangan Berpangkat Sebenarnya
Bilangan berpangkat sebenarnya adalah bilangan yang diperoleh dengan melakukan perkalian berulang.
Contoh:
2. Bilangan Berpangkat Tak Sebenarnya
Bilangan berpangkat tak sebenarnya adalah bilangan berpangkat yang tidak dapat diperoleh dengan perkalian berulang.
Contoh: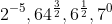
Dengan demikian, bilangan berpangkat yaitu bilangan berpangkat bulat positif. Adapun bilangan berpangkat tak sebenarnya meliputi bilangan berpangkat bilangan bulat negatif, nol dan pecahan.
Sifat-sifat perpangkatan bilangan.
1. Sifat distributif perpangkatan terhadap perkalian.
2. Perkalian bilangan berpangkat.
3. Pembagian bilangan berpangkat.
4. Sifat distributif perpangkatan terhadap bilangan berpangkat.
5. Bila a bilangan real sedangkan m dan n adalah bilangan bulat positif yang memenuhi m ≥ n, maka berlaku:
6. Bila a bilangan bulat sedangkan m dan n adalah bilangan bulat positif yang memenuhi m ≥ n, maka berlaku:
7. Fungsi bilangan nol (0) dalam perpangkatan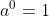 , dengan a bilangan real.
, dengan a bilangan real.
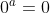
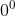 tidak terdefinisikan
tidak terdefinisikan
Catatan:
^p{}=a^p{}) , untuk p bilangan genap,
, untuk p bilangan genap,
^p{}=-(a)^p{}) , untuk p bilangan ganjil,
, untuk p bilangan ganjil,
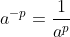
Bentuk Akar
Bilangan real terdiri dari dua jenis bilangan yaitu bilangan rasional dan irasional.
Bilangan Rasional
Bilanagn rasional adalah bilangan yang dapat dinyatakan ke dalam bentuk a/b dengan a, b merupakan anggota bilangan bulat, dan b ≠ 0. Contoh: . Sifat-sifat yang berlaku pada bilangan bulat berpangkat bilangan bulat berlaku juga pada bilangan rasional berpangkat bulat.
. Sifat-sifat yang berlaku pada bilangan bulat berpangkat bilangan bulat berlaku juga pada bilangan rasional berpangkat bulat.
Contoh:
^2{x\left ( \frac{3}{5} \right )^7{}}}{}\left ( \frac{3}{5} \right )^{6})
^2^{+7^-{6}{}}{})
^3{})
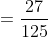
2. Bilangan Irasional
Bilangan irasional adalah bilangan yang dapat dinyatakan ke dalam bentuk a/b dengan a, b merupakan anggota bilangan bulat, dan b ≠ 0. Contoh: √3,√5,√7. Bentuk bilangan seperti √3,√5,√7 disebut bentuk akar.
Sifat-sifat bentuk akar seperti berikut.
1. √ab=√a x √b , dengan a dan b merupakan bilangan real positif.
Contoh: √21=√(7 ) x √3
2. √(a/b)=√a/√b , dengan a≥0 dan b>0
Contoh: √(2/6)=√2/√6=√2/(√2 x √3)=1/√3
Operasi aljabar pada bentuk akar mempunyai sifat-sifat seperti berikut.
1. a√c+b√c=(a+b)√c , dengan a, b, c bilangan real dan c ≥0.
2. a√c-b√c=(a-b)√c , dengan a, b, c bilangan real dan c ≥0.
3. a√c x b√c=(ab)√cd , dengan a, b, c, d bilangan real dengan a ≥0 dan b ≥0.
4. (c√a)/(d√b)=c/d √(a/b) , dengan a, b, c, d bilangan real dengan a ≥0 dan b ≥0.
Bentuk akar a/√b dapat dirasionalkan dengan cara mengalikan pembilang dengan penyebut pecahan tersebut, dengan bentuk sekawan penyebutnya.
Caranya seperti berikut: a/√b=a/√b x √b/√b=a/b √b
Bentuk akar c/(√a+√b) juga dapat dirasionalkan dengan cara yang sama. Sekawan penyebut √a+√b adalah √a-√b. Sehingga cara merasionalkan bentuk akar c/(√a+√b) dapat dituliskan seperti berikut.
c/(√a+√b)=c/(√a+√b) x (√a-√b)/(√a-√b)=(c(√a-√b))/(a-b)
Catatan:
Bila penyebutnya adalah √a-√b , maka bentuk sekawannya adalah √a-√b.
A. Bilangan Berpangkat
Bilangan berpangkat dibedakan menjadi dua macam, sebagai berikut.
1. Bilangan Berpangkat Sebenarnya
Bilangan berpangkat sebenarnya adalah bilangan yang diperoleh dengan melakukan perkalian berulang.
Contoh:
2. Bilangan Berpangkat Tak Sebenarnya
Bilangan berpangkat tak sebenarnya adalah bilangan berpangkat yang tidak dapat diperoleh dengan perkalian berulang.
Contoh:
Dengan demikian, bilangan berpangkat yaitu bilangan berpangkat bulat positif. Adapun bilangan berpangkat tak sebenarnya meliputi bilangan berpangkat bilangan bulat negatif, nol dan pecahan.
Sifat-sifat perpangkatan bilangan.
1. Sifat distributif perpangkatan terhadap perkalian.
2. Perkalian bilangan berpangkat.
3. Pembagian bilangan berpangkat.
4. Sifat distributif perpangkatan terhadap bilangan berpangkat.
5. Bila a bilangan real sedangkan m dan n adalah bilangan bulat positif yang memenuhi m ≥ n, maka berlaku:
6. Bila a bilangan bulat sedangkan m dan n adalah bilangan bulat positif yang memenuhi m ≥ n, maka berlaku:
7. Fungsi bilangan nol (0) dalam perpangkatan
Catatan:
Bentuk Akar
Bilangan real terdiri dari dua jenis bilangan yaitu bilangan rasional dan irasional.
Bilangan Rasional
Bilanagn rasional adalah bilangan yang dapat dinyatakan ke dalam bentuk a/b dengan a, b merupakan anggota bilangan bulat, dan b ≠ 0. Contoh:
Contoh:
2. Bilangan Irasional
Bilangan irasional adalah bilangan yang dapat dinyatakan ke dalam bentuk a/b dengan a, b merupakan anggota bilangan bulat, dan b ≠ 0. Contoh: √3,√5,√7. Bentuk bilangan seperti √3,√5,√7 disebut bentuk akar.
Sifat-sifat bentuk akar seperti berikut.
1. √ab=√a x √b , dengan a dan b merupakan bilangan real positif.
Contoh: √21=√(7 ) x √3
2. √(a/b)=√a/√b , dengan a≥0 dan b>0
Contoh: √(2/6)=√2/√6=√2/(√2 x √3)=1/√3
Operasi aljabar pada bentuk akar mempunyai sifat-sifat seperti berikut.
1. a√c+b√c=(a+b)√c , dengan a, b, c bilangan real dan c ≥0.
2. a√c-b√c=(a-b)√c , dengan a, b, c bilangan real dan c ≥0.
3. a√c x b√c=(ab)√cd , dengan a, b, c, d bilangan real dengan a ≥0 dan b ≥0.
4. (c√a)/(d√b)=c/d √(a/b) , dengan a, b, c, d bilangan real dengan a ≥0 dan b ≥0.
Bentuk akar a/√b dapat dirasionalkan dengan cara mengalikan pembilang dengan penyebut pecahan tersebut, dengan bentuk sekawan penyebutnya.
Caranya seperti berikut: a/√b=a/√b x √b/√b=a/b √b
Bentuk akar c/(√a+√b) juga dapat dirasionalkan dengan cara yang sama. Sekawan penyebut √a+√b adalah √a-√b. Sehingga cara merasionalkan bentuk akar c/(√a+√b) dapat dituliskan seperti berikut.
c/(√a+√b)=c/(√a+√b) x (√a-√b)/(√a-√b)=(c(√a-√b))/(a-b)
Catatan:
Bila penyebutnya adalah √a-√b , maka bentuk sekawannya adalah √a-√b.





Komentar
Posting Komentar