KESEBANGUNAN DAN KEKONGRUENAN BANGUN DATAR
A. Kesebangunan Bangun Datar
1. Dua Bangun Datar yang Sebangun
Dua bangun datar dikatakan sebangun bila memenuhi syarat-syarat berikut:
a. Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai.
b. Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar.
Contoh:
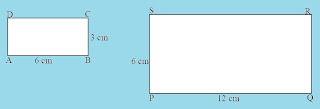
Perhatikan bangun persegi panjang ABCD dan bangun persegi panjang PQRS.
- Ukuran persegi panjang ABCD dan persegi panjang PQRS.
Perbandingan panjang kedua bangun di atas adalah:
Perbandingan lebar kedua bangun di atas adalah:
- Besar sudut-sudut pada persegi panjang ABCD dan persegi panjang PQRS.
Kedua bangun tersebut merupakan bangun persegi panjang, sehingga setiap sudutnya merupakan sudut siku-siku. Diperoleh:
Dengan demikian, karena:
- Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai
- Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar
Maka persegi panjang ABCD sebangun dengan persegi panjang PQRS.
2. Dua Segitiga yang Sebangun
Khusus untuk segitiga, dua segitiga dikatakan sebangun bila elah memenuhi syarat-syarat berikut.
a. Panjang sisi-isi yang bersesuaian memiliki perbandingan yang sama. Syarat ini disingkat s.s.s (sisi-sisi-sisi).
b. Sudut-sudut ysng bersesuaian sama besar. Syarat ini disingkat sd.sd.sd (sudut-sudut-sudut).
c. Dua sisi yang bersesuaian memiliki perbandingan yang sama dan sudut bersesuaian yang diapit sama besar. Syarat ini disingkat s.sd.s (sisi-sudut-sisi).
Kesebangunan dinotasikan dengan " ".
".
Contoh:
Diketahui panajang CD = 12 cm, AD = 6 cm dan AB = 9 cm. Tentukan panjang DE!
Buktikan segitiga ABC sebangun dengan segitiga DEC.
Bukti:
Perhatikan segitiga ABC dan segitiga DEC
Dengan demikian, terpenuhi syarat sd.sd.sd sehingga segitiga ABC sebangun dengan segitiga DEC, atau:
Segitiga ABC segitiga DEC.
segitiga DEC.
Berlaku perbandingan:
Sehingga
Jadi, panjang DE adalah 6 cm.
B. Kekongruenan Bangun Datar
Dua benda atau lebih yang memiliki bentuk dan ukuran yang sama disebut kongruen. Kekongruenan dinotasikan dengan lambang " ".
".
1. Dua Bangun Datar yang Kongruen
Dua bangun atau lebih dikatakan kongruen jika bangun-bangun tersebut memiliki bentuk dan ukuran yang sama serta sudut-sudut yang bersesuaian sama besar.
Contoh:
Diketahui panjang AB = RS, BC = PS, CD = PQ, AD = QR, ,
,  dan
dan  . Tentukan besar sudut R!
. Tentukan besar sudut R!
Jawab:
Agar dapat menemtukan besar sudut R, terlebih dahulu kita buktikan bangun trapesium ABCD kongruen dengan bangun trapesium PQRS.
Bukti:
Berdasarkan gambar diperoleh keterangan bahwa panjang:
AB = RS BC = PS
CD = PQ AD = QR
Panjang sisi-sisi pada bangun trapesium ABCD ternyata sama panjang atau bersesuaian dengan panjang sisi-sisi bangun trapesium PQRS.
Jadi, terbukti jika bangun trapesium ABCD kongruen dengan bangun trapesium PQRS, atau:
Trapesium ABCD trapesium PQRS.
trapesium PQRS.
Berdasarkan sifat-sifat kekongruenan yang berlaku maka:
Pada trapesium berlaku jumlah besar keempat sudutnya adalah 360°.
Dengan demikian,
 =360°-(105°+65°+75°)
=360°-(105°+65°+75°)
= 360°-245° = 115°
Jadi, besar sudut = 115°
= 115°
2. Dua Segitiga yang Kongruen
Bila dua buah segitiga kongruen maka dua segitiga tersebut dapat saling menutupi secara tepat.
Dua buah segitiga dikatakan kongruen bila memenuhi syarat-syarat berikut:
a. Sisi-sisi yang bersesuaian sama panjang, disingkat s.s.s (sisi-sisi-sisi).
b. Dua sisi yang bersesuaian sama panjang dan satu sudut yang diapit oleh kedua sisi tersebut sama besar, disingkat s.sd.s (sisi-sudut-sisi).
c. Dua sudut yang bersesuaian sama besar dan satu sisi yang bersesuaian sama panjang, disingkat sd.s.sd (sudut-sisi-sudut).
Contoh:
Buktikan segitiga ABC kongruen dengan segitiga DEF!
Bukti:
Perhatikan segitiga DEF.
Segitiga DEF merupakan segitiga siku-siku, sehingga untuk mencari panjang EF dapat digunakan rumus Phytagoras.
Panjang EF adalah 12 cm
Perhatikan kembali segitiga ABC dengan segitiga DEF!
AC = DE = 5 cm
 = sudut siku-siku = 90°
= sudut siku-siku = 90°
AB = EF = 12 cm
Dengan demikian, syarat dua sisi yang bersesuaian sama panjang dan satu sudut yang diapit oleh kedua sisi sisi tersebut sama besar, disingkat s.sd.s (sisi-ssudut-sisi) terpenuhi.
A. Kesebangunan Bangun Datar
1. Dua Bangun Datar yang Sebangun
Dua bangun datar dikatakan sebangun bila memenuhi syarat-syarat berikut:
a. Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai.
b. Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar.
Contoh:
Perhatikan bangun persegi panjang ABCD dan bangun persegi panjang PQRS.
- Ukuran persegi panjang ABCD dan persegi panjang PQRS.
Perbandingan panjang kedua bangun di atas adalah:
Perbandingan lebar kedua bangun di atas adalah:
- Besar sudut-sudut pada persegi panjang ABCD dan persegi panjang PQRS.
Kedua bangun tersebut merupakan bangun persegi panjang, sehingga setiap sudutnya merupakan sudut siku-siku. Diperoleh:
Dengan demikian, karena:
- Panjang sisi-sisi yang bersesuaian pada bangun-bangun tersebut memiliki perbandingan yang senilai
- Sudut-sudut yang bersesuaian pada bangun-bangun tersebut sama besar
Maka persegi panjang ABCD sebangun dengan persegi panjang PQRS.
2. Dua Segitiga yang Sebangun
Khusus untuk segitiga, dua segitiga dikatakan sebangun bila elah memenuhi syarat-syarat berikut.
a. Panjang sisi-isi yang bersesuaian memiliki perbandingan yang sama. Syarat ini disingkat s.s.s (sisi-sisi-sisi).
b. Sudut-sudut ysng bersesuaian sama besar. Syarat ini disingkat sd.sd.sd (sudut-sudut-sudut).
c. Dua sisi yang bersesuaian memiliki perbandingan yang sama dan sudut bersesuaian yang diapit sama besar. Syarat ini disingkat s.sd.s (sisi-sudut-sisi).
Kesebangunan dinotasikan dengan "
Contoh:
Diketahui panajang CD = 12 cm, AD = 6 cm dan AB = 9 cm. Tentukan panjang DE!
Buktikan segitiga ABC sebangun dengan segitiga DEC.
Bukti:
Perhatikan segitiga ABC dan segitiga DEC
Dengan demikian, terpenuhi syarat sd.sd.sd sehingga segitiga ABC sebangun dengan segitiga DEC, atau:
Segitiga ABC
Berlaku perbandingan:
Sehingga
Jadi, panjang DE adalah 6 cm.
B. Kekongruenan Bangun Datar
Dua benda atau lebih yang memiliki bentuk dan ukuran yang sama disebut kongruen. Kekongruenan dinotasikan dengan lambang "
1. Dua Bangun Datar yang Kongruen
Dua bangun atau lebih dikatakan kongruen jika bangun-bangun tersebut memiliki bentuk dan ukuran yang sama serta sudut-sudut yang bersesuaian sama besar.
Contoh:
Diketahui panjang AB = RS, BC = PS, CD = PQ, AD = QR,
Jawab:
Agar dapat menemtukan besar sudut R, terlebih dahulu kita buktikan bangun trapesium ABCD kongruen dengan bangun trapesium PQRS.
Bukti:
Berdasarkan gambar diperoleh keterangan bahwa panjang:
AB = RS BC = PS
CD = PQ AD = QR
Panjang sisi-sisi pada bangun trapesium ABCD ternyata sama panjang atau bersesuaian dengan panjang sisi-sisi bangun trapesium PQRS.
Jadi, terbukti jika bangun trapesium ABCD kongruen dengan bangun trapesium PQRS, atau:
Trapesium ABCD
Berdasarkan sifat-sifat kekongruenan yang berlaku maka:
Pada trapesium berlaku jumlah besar keempat sudutnya adalah 360°.
Dengan demikian,
= 360°-245° = 115°
Jadi, besar sudut
2. Dua Segitiga yang Kongruen
Bila dua buah segitiga kongruen maka dua segitiga tersebut dapat saling menutupi secara tepat.
Dua buah segitiga dikatakan kongruen bila memenuhi syarat-syarat berikut:
a. Sisi-sisi yang bersesuaian sama panjang, disingkat s.s.s (sisi-sisi-sisi).
b. Dua sisi yang bersesuaian sama panjang dan satu sudut yang diapit oleh kedua sisi tersebut sama besar, disingkat s.sd.s (sisi-sudut-sisi).
c. Dua sudut yang bersesuaian sama besar dan satu sisi yang bersesuaian sama panjang, disingkat sd.s.sd (sudut-sisi-sudut).
Contoh:
Buktikan segitiga ABC kongruen dengan segitiga DEF!
Bukti:
Perhatikan segitiga DEF.
Segitiga DEF merupakan segitiga siku-siku, sehingga untuk mencari panjang EF dapat digunakan rumus Phytagoras.
Panjang EF adalah 12 cm
Perhatikan kembali segitiga ABC dengan segitiga DEF!
AC = DE = 5 cm
AB = EF = 12 cm
Dengan demikian, syarat dua sisi yang bersesuaian sama panjang dan satu sudut yang diapit oleh kedua sisi sisi tersebut sama besar, disingkat s.sd.s (sisi-ssudut-sisi) terpenuhi.











Komentar
Posting Komentar