POLA BILANGAN, BARISAN DAN DERET
POLA BILANGAN, BARISAN DAN DERET
A. Pola Bilangan
Suatu pola bilangan dapat mewakili bilangan-bilangan tertentu. Pola bilangan bermacam-macam, diantaranya pola garis lurus, pola persegi panjang, pola persegi, pola segitiga, pola bilangan ganjil dan genap serta pola segitiga pascal.
1. Pola Garis Lurus
Pola garis lurus merupakan pola bilangan yang paling sederhana. Pola noktahnya dibentuk seperti garis lurus. Contohnya sebagai berikut.
2. Pola Persegi Panjang
Pola bilangan persegi panjang noktahnya dapat dibentuk seperti persegi panjang. Contohnya sebagai berikut.
3. Pola Persegi
Pola bilangan persegi noktahnya dibentuk seperti persegi, setiap sisinya harus sama panjang. Contohnya sebagai berikut.
Bila pola persegi terus dilanjutkan akan membentuk barisan bilangan kuadrat berikut. 1, 4, 9, 16, 25, 36, …
4. Pola Segitiga
Pola bilangan juga dapat digambarkan membentuk segitiga. Contohnya seperti berikut.
Bila pola segitiga terus dilanjutukan akan membentuk barisan bilangan berikut. 1, 3, 6, 10, 15, 21, 28, …
5. Pola Bilangan Ganjil dan Genap
Bilangan dapat dibagi menjadi dua macam, yaitu bilangan ganjil dan bilangan genap.
a. Bilangan ganjil
Bilangan ganjil dimulai dari angka 1. Bilangan selanjutnya adalah bilangan 1 ditambah 2, bilangan selanjutnya adalah bilangan hasil dari (1 + 2 yang ditambahkan 2, dan seterusnya). Dengan demikian, bilangan ganjil dapat dituliskan sebagai berikut. 1, 3, 5, 7, 9, 11, 13, 15, 17, …
b. Bilangan genap
Bilangan genap dimulai dari 2. Bilangan genap dituliskan seperti berikut. 2, 4, 6, 8, 10, 12, 14, 16, 18, …
6. Pola Segitiga Pascal
Pola bilangan Segitiga Pascal berbeda dengan pla bilangan sebelumnya. Pola bilangan pascal selalu dimulai dari angka 1 dan diakhiri dengan angka 1. Bentuknya seperti berikut.
B. Barisa Bilangan
Barisan bilangan dapat membentuk pola tertentu. Berdasarkan polanya, barisan bilangan dibagi menjadi dua bagian, yaitu Barisan aritmetika(barisan hitung) dan Barisa geometri (barisan ukur).
1. Barisan Aritmetika
Barisan aritmetika adalah barisan yang mempunyai selisih sama antara bilangan yang saling berdekatan. Selisih tersebut disebut beda yang dilambangkan b. Beda barisan aritmetika dapat berupa bilangan positif maupun bilangan negatif. Barisan aritmetika dibedakan menjadi dua macam.
a. Barisan aritmetika naik
Bila bedanya positif maka disebut barisan aritmetika naik.
Contoh: barisan 3, 6, 9, 12, 15, … mempunyai beda (b) = 3
b. Barisan bilangan turun
Bila bedanya negatif maka disebut barisan aritmetika turun.
Contoh: barisan 36, 31, 26, 21, 16, 11, … mempunyai beda (b) = -5
Bila diketahui barisan aritmetika seperti berikut.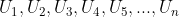
2. Barisan Geometri
Barisan geometri disebut juga barisan ukur. Barisan geometri adalah barisan bilangan yang memiliki rasio tetap antara dua suku barisan yang berurutan. Suku barisan diperoleh dari suku sebelumnya dengan cara mengalikan atau membagi dengan bilangan yang sama. Bilangan tetap tersebut disebut rasio. Rasio dilambangkan r. Barisan geometri dibedakan menjadi dua macam.
Barisan geometri naik
Barisan geometri naik mempunyai r > 1. Barisan geometri naik disebut juga barisan divergen.
Contoh: 2, 4, 8, 16, 32, 64, … mempunyai rasio (r) = 2.
Jadi, barisan 2, 4, 8, 16, 32, 64, … merupakan barisan geomtri naik atau barisan divergen
Barisan geometri turun
Barisan geometri turun mempunyai r < 1. Barisan goemetri turun disebut juga barisan konvergen. Contoh: 96, 48, 24, 12, 6, 3, 3/2, … mempunyai rasio (r) = 1/2. Jadi, barisan 96, 48, 24, 12, 6, 3, 3/2, … merupakan barisan geometri turun atau barisan konvergen. Misalkan, terdapat barisan geometri berikut.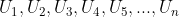
C. Deret Bilangan
Deret bilangan adalah jumlah dari suku-suku barisan bilangan. Deret bilangan dinyatakan dengan S_n. Deret bilangan dibedakan menjadi dua macam, yaitu deret aritmetika dan deret geometri.
1. Deret aritmetika
Deret aritmetika disebut juga deret hitung. Deret aritmetika adalah jumlah dari suku-suku barisan aritmetika. Dengan demikian, jumlah suku-suku deret aritmetika adalah:
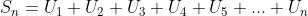
+\left ( a+2b \right )+\left ( a+3b \right )+\left ( a+4b \right )+...+\left ( a\left ( n-1 \right )b \right ))
Jumlah suku-suku barisan aritmetika dapat dihitung dengan rumus berikut:
Perlu diingat, dalam deret aritmetika berlaku sebagai berikut.
- Bila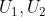 dan
dan 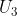 merupakan deret aritmetika maka berlaku:
merupakan deret aritmetika maka berlaku:
- Bila dan
dan 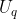 merupakan suku-suku dalam deret aritmetika maka berlaku:
merupakan suku-suku dalam deret aritmetika maka berlaku:
2. Deret geometri
Deret geometri disebut juga deret ukur. Deret geometri adalah jumlah dari suku-suku deret geometri. Dengan demikian, jumlah suku-suku deret geometri adalah:
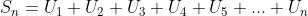
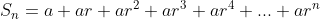
Jumlah suku-suku barisan geometri dapat dihitung dengan rumus berikut:
Dalam deret geometri berlaku sebagai berikut.
Kuadrat suku tengah = hasil kali suku tepi.
Bila dan
dan 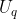 merupakan suku-suku dalam deret goemetri maka berlaku:
merupakan suku-suku dalam deret goemetri maka berlaku:
A. Pola Bilangan
Suatu pola bilangan dapat mewakili bilangan-bilangan tertentu. Pola bilangan bermacam-macam, diantaranya pola garis lurus, pola persegi panjang, pola persegi, pola segitiga, pola bilangan ganjil dan genap serta pola segitiga pascal.
1. Pola Garis Lurus
Pola garis lurus merupakan pola bilangan yang paling sederhana. Pola noktahnya dibentuk seperti garis lurus. Contohnya sebagai berikut.
2. Pola Persegi Panjang
Pola bilangan persegi panjang noktahnya dapat dibentuk seperti persegi panjang. Contohnya sebagai berikut.
3. Pola Persegi
Pola bilangan persegi noktahnya dibentuk seperti persegi, setiap sisinya harus sama panjang. Contohnya sebagai berikut.
Bila pola persegi terus dilanjutkan akan membentuk barisan bilangan kuadrat berikut. 1, 4, 9, 16, 25, 36, …
4. Pola Segitiga
Pola bilangan juga dapat digambarkan membentuk segitiga. Contohnya seperti berikut.
Bila pola segitiga terus dilanjutukan akan membentuk barisan bilangan berikut. 1, 3, 6, 10, 15, 21, 28, …
5. Pola Bilangan Ganjil dan Genap
Bilangan dapat dibagi menjadi dua macam, yaitu bilangan ganjil dan bilangan genap.
a. Bilangan ganjil
Bilangan ganjil dimulai dari angka 1. Bilangan selanjutnya adalah bilangan 1 ditambah 2, bilangan selanjutnya adalah bilangan hasil dari (1 + 2 yang ditambahkan 2, dan seterusnya). Dengan demikian, bilangan ganjil dapat dituliskan sebagai berikut. 1, 3, 5, 7, 9, 11, 13, 15, 17, …
b. Bilangan genap
Bilangan genap dimulai dari 2. Bilangan genap dituliskan seperti berikut. 2, 4, 6, 8, 10, 12, 14, 16, 18, …
6. Pola Segitiga Pascal
Pola bilangan Segitiga Pascal berbeda dengan pla bilangan sebelumnya. Pola bilangan pascal selalu dimulai dari angka 1 dan diakhiri dengan angka 1. Bentuknya seperti berikut.
B. Barisa Bilangan
Barisan bilangan dapat membentuk pola tertentu. Berdasarkan polanya, barisan bilangan dibagi menjadi dua bagian, yaitu Barisan aritmetika(barisan hitung) dan Barisa geometri (barisan ukur).
1. Barisan Aritmetika
Barisan aritmetika adalah barisan yang mempunyai selisih sama antara bilangan yang saling berdekatan. Selisih tersebut disebut beda yang dilambangkan b. Beda barisan aritmetika dapat berupa bilangan positif maupun bilangan negatif. Barisan aritmetika dibedakan menjadi dua macam.
a. Barisan aritmetika naik
Bila bedanya positif maka disebut barisan aritmetika naik.
Contoh: barisan 3, 6, 9, 12, 15, … mempunyai beda (b) = 3
b. Barisan bilangan turun
Bila bedanya negatif maka disebut barisan aritmetika turun.
Contoh: barisan 36, 31, 26, 21, 16, 11, … mempunyai beda (b) = -5
Bila diketahui barisan aritmetika seperti berikut.
2. Barisan Geometri
Barisan geometri disebut juga barisan ukur. Barisan geometri adalah barisan bilangan yang memiliki rasio tetap antara dua suku barisan yang berurutan. Suku barisan diperoleh dari suku sebelumnya dengan cara mengalikan atau membagi dengan bilangan yang sama. Bilangan tetap tersebut disebut rasio. Rasio dilambangkan r. Barisan geometri dibedakan menjadi dua macam.
Barisan geometri naik
Barisan geometri naik mempunyai r > 1. Barisan geometri naik disebut juga barisan divergen.
Contoh: 2, 4, 8, 16, 32, 64, … mempunyai rasio (r) = 2.
Jadi, barisan 2, 4, 8, 16, 32, 64, … merupakan barisan geomtri naik atau barisan divergen
Barisan geometri turun
Barisan geometri turun mempunyai r < 1. Barisan goemetri turun disebut juga barisan konvergen. Contoh: 96, 48, 24, 12, 6, 3, 3/2, … mempunyai rasio (r) = 1/2. Jadi, barisan 96, 48, 24, 12, 6, 3, 3/2, … merupakan barisan geometri turun atau barisan konvergen. Misalkan, terdapat barisan geometri berikut.
C. Deret Bilangan
Deret bilangan adalah jumlah dari suku-suku barisan bilangan. Deret bilangan dinyatakan dengan S_n. Deret bilangan dibedakan menjadi dua macam, yaitu deret aritmetika dan deret geometri.
1. Deret aritmetika
Deret aritmetika disebut juga deret hitung. Deret aritmetika adalah jumlah dari suku-suku barisan aritmetika. Dengan demikian, jumlah suku-suku deret aritmetika adalah:
Jumlah suku-suku barisan aritmetika dapat dihitung dengan rumus berikut:
Perlu diingat, dalam deret aritmetika berlaku sebagai berikut.
- Bila
- Bila
2. Deret geometri
Deret geometri disebut juga deret ukur. Deret geometri adalah jumlah dari suku-suku deret geometri. Dengan demikian, jumlah suku-suku deret geometri adalah:
Jumlah suku-suku barisan geometri dapat dihitung dengan rumus berikut:
Dalam deret geometri berlaku sebagai berikut.
Kuadrat suku tengah = hasil kali suku tepi.
Bila
















Komentar
Posting Komentar